Published : 21 Jul 2014 06:33 PM
Last Updated : 21 Jul 2014 06:33 PM
உயிரினங்களை புரிந்துகொள்ள வைக்கும் கிளைபர் அதிசய கணித விதி
கணிதம் எவ்வாறு உயிரினங்களை புரிந்து கொள்ள துணை புரிகிறது என்பதை பார்ப்போம். குறிப்பாக “அலோமெட்ரி” என்பது உயிரினங்களின் மாற்றங்களை அதன் உடல் வளர்ச்சிக்கேற்ப விளக்கும் பண்பை குறிக்கும். உதாரணமாக சிறிய அளவில் தோன்றும் ஒரு எலி முதல் பெரிய அளவில் தோன்றும் யானை வரை உயிரினங்களின் உடல் அளவு அதிகரிப்பதற்கேற்றவாறு அவ்வுயிரினங்களின் இதயத் துடிப்பு குறைவாக அமையும், எலும்புகள் குறுகி மெல்லிய அளவில் காணப்படும், மூளை பெரிதாக அமையும், ஆயுட்காலம் அதிகரிக்கும். எனவே ஒரு உயிரினத்தின் உடல் அளவுக்கேற்றவாறு அதன் அடிப்படை அம்சங்கள் அமையும் என்பதைத் தான் “அலோமெட்ரி” விளக்குகிறது.
ஒரு எலி ஏறக்குறைய ஒரு யானையின் இதயத்துடிப்பின் சமமான அளவிற்கு இதயத்துடிப்பை தன் வாழ்நாளில் ஏற்படுத்துகிறது. ஆனால் எலி அநேகமாக ஒரு வருட காலமே உயிர் வாழ, யானையோ கிட்டத்தட்ட ஐம்பது ஆண்டுகளுக்கு மேல் உயிர் வாழ்கிறது. எலியும், யானையும் ஒரே அளவிலாளான இதயத்துடிப்பை பெற்றிருந்தாலும் யானையால் எவ்வாறு எலியைவிட ஐம்பது மடங்கிற்கு மேலான காலத்திற்கு உயிர் வாழ முடிகிறது? இதற்கு யானையின் பெரிய உருவ அமைப்பு மட்டுமே காரணமா?
அதேபோல் சிறிய அளவிலான செடிகளும், விலங்குகளும் எவ்வாறு அதனை விடப் பெரிய அளவில் அமைந்த செடிகளை, விலங்குகளை விட விரைவில் வளர்ச்சியுறுகின்றன? செடிகளின் வளர்ச்சிக்கும், விலங்குகளின் வளர்ச்சிக்கும் ஏதேனும் தொடர்பு உண்டா? இயற்கை அனைத்து அம்சங்களையும் ஏதேனும் ரகசிய செயல்பாட்டிற்கு உட்படுத்தி இயக்குகிறதா? இது போன்ற கேள்விகளுக்கு எளிதில் விடை காண முடிவதில்லை. ஆனால் சிறிது ஆய்வு புரிந்தால் இதற்கான விடையை கணிதத்தின் துணை கொண்டு ஓரளவிற்கு புரிந்து கொள்ளலாம்.
மேற்கண்ட கேள்விகளுக்கான விடைகளை தெரிந்து கொள்ள முதலில் நாம் சுவிட்சர்லாந்து நாட்டு உயிரியல் அறிஞர் மேக்ஸ் க்ளைபர், 1932 ல் வழங்கிய அரிய சூத்திரத்தை காண வேண்டும். “எல்லா உயிரினங்களின் வளர்சிதை மாற்றமும் அதன் நிறையின் நான்கில் மூன்று மடங்கு படியில் அமையும்” என்பதே க்ளைபர் விதி என்ற புகழ்பெற்ற உயிரியல் விதியாகும். ஒரு உயிரினத்தின் வளர்சிதை மாற்றத்தை E எனவும், அதன் நிறையை M என கருதினால் க்ளைபர் விதிப்படி நாம் பெறுவது என்ற கணித சூத்திரமாகும்.
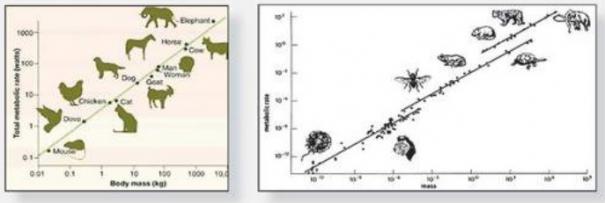
மிகச் சிறிய அளவிலான நுண்ணுயிர்கள் முதல் மிகப் பெரிய அளவு கொண்ட உயிரினங்கள் வரை அனைத்து உயிரினங்களுக்கும், தாவரங்களுக்கும் பொருந்துவதே இவ்விதியின் அதிசயமாக உயிரியல் வல்லுநர்கள் கருதுகிறார்கள். இதை படத்தில் காணலாம்.
உயிரினங்களின் அடிப்படை வடிவத்தை கோளமாக கருதிக் கொண்டால் கணித கணக்கீட்டின் படி “ஒரு உயிரினத்தின் வளர்சிதை மாற்றம் அதன் நிறையின் மூன்றின் இரு மடங்கு படியில் தான் அமைய வேண்டும்”. அதாவது என்றே அமைய வேண்டும். ஆனால் அனைத்து உயிரினங்களும், தாவிரங்களும் க்ளைபர் விதிப்படியே நிறையின் படியாக விளங்கும் ரகசியத்தை வெகு காலமாக அறிவியல் அறிஞர்களால் புரிந்து கொள்ள முடியவில்லை என்றே கூறலாம். இறுதியாக 1997 ல் தான் க்ளைபர் விதியில் அமைந்த அதிசய படியின் விளக்கத்தை மூன்று அறிஞர்கள் வழங்கினார்கள்.
இந்த விளக்கத்திற்கு அவர்கள் பயன்படுத்திய சிந்தனையை “பகுவியல் ஜியோமிதி” (“Fractal Geometry”) என்று கணிதத்தில் அழைப்போம். பகுவியல் ஜியோமிதி, வெவ்வேறு அளவிலாளான சுய வடிவொப்புமை என்ற மிகச் சிறந்த பண்பை பெற்று விளங்கும் கணித உட்பிரிவாகும். இதன்படி, ஒரே வடிவத்தை கொண்ட பொருள் வெவ்வேறு அளவில் தோன்றும் பண்பை பெறும். இதை படத்தில் காணலாம்.
பகுவியல் ஜியோமிதி என்ற கணித சிந்தனையை கொண்டு க்ளைபர் விதியில் தோன்றும் படிக்கு விளக்கத்தை அளிக்க முடிந்தது. இத்தீர்வில் உயிரினங்களின் இரத்த ஓட்டத்தை ஒரு முக்கிய காரணியாக கருதியே நிரூபித்தனர். ஆனால் பாக்டீரியா, பவளம் போன்ற இரத்த ஓட்டமே இல்லாத நுண்ணியிர்களுக்கும் இவ்விதி பொருந்துவதை மேற்கூறிய விளக்கத்தால் பெறமுடியவில்லை.
எனவே அனைத்து உயிரினங்களுக்கும் தாவிரங்களுக்கும், பொருந்துமாறு சரியான விளக்கத்தை தேட உயிரியல் அறிஞர்கள் முற்பட்டனர். அண்மையில் பகுமுறை ஜியோமிதியை கருதாமல், எல்லா அம்சங்களுக்கும் பொருந்துமாறு விளங்கும் தீர்வு வழங்கப்பட்டுள்ளது. இரத்த ஓட்ட பிணையத்தில் தோன்றும் வளர்சிதை மாற்றத்தை கருதி க்ளைபர் விதிக்கு பொதுத் தீர்வை இன்று அறிஞர்கள் கண்டறிந்துள்ளனர்.
என்ற கணித சமன்பாட்டின் மூலம் பல்வேறு உயிரியல் சார்ந்த செய்திகளை நாம் அறிய முடிகிறது. எளிமையான கணித சூத்திரம் கொண்டு நுண்ணியிர் முதல் வெவ்வேறு உயிரினங்கள், தாவரங்கள் போன்றவற்றின் பண்பை அறிவதை காணும் பொழுது இன்றளவும் அறிவியல் அறிஞர்களுக்கு வியப்பாகவே உள்ளது. க்ளைபர் விதி உண்மையில் பரிணாம வளர்ச்சியை விளக்கும் எளிமையான விதியாக விளங்குவதை நாம் இதன் மூலம் உணரலாம்.
FOLLOW US
Sign up to receive our newsletter in your inbox every day!


WRITE A COMMENT