அறிவியல் அறிவோம்- 7: பூமியைத் துளைத்து வெளியேறுமா கல்?

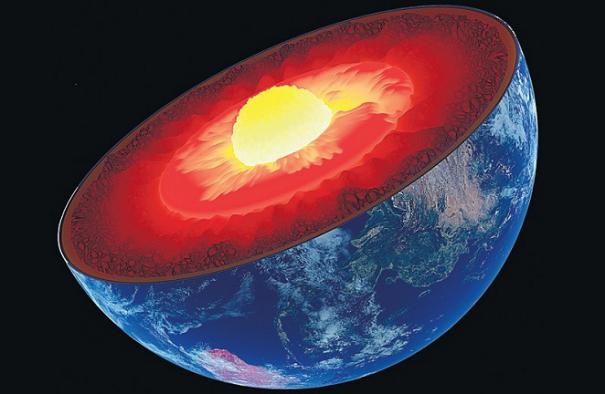
அற்புத உலகில் ஆலிஸ் என்ற நாவலில் முயலின் வளைக்குள் விழுந்து பூமிக்குள் செல்வாள் ஆலிஸ். “ இப்படியே போய் பூமியின் மறுபுறத்தில் வெளிவந்துவிடுவேனா?” என வியந்துபோவாள். கலிலியோ உட்பட பல விஞ்ஞானிகள் பூமியின் ஊடே துளை போட்டு அதில் ஒரு கல்லை நழுவ விட்டால் என்ன ஆகும் என வியந்துள்ளனர்.

பூமியில் துளை

சாதாரணமாக 100 அடி ஆழத்துக்குக் கிணறு வெட்டுவோம். அதையே 12 ஆயிரம் கி.மீ. ஆழத்துக்குக் வெட்டினால் என்ன ஆகும்? அந்தத் துளைக்குள் ஒரு கல்லைப் போட்டால் என்ன ஆகும்?

அப்படி எல்லாம் உண்மையில் பூமியைத் துளைத்து மறு பக்கம் வருவது போல கிணறு வெட்ட முடியாது. பூமிக்குள் இருக்கும் மிகு அதிக அழுத்தம், மிக அதிக வெப்பம் ஆகியவற்றைச் சமாளித்து எப்படித் துளை போட முடியும் என்பது ஒருபக்கம் இருக்கட்டும். பூமியின் மையம் பாகு நிலையில் கொழ கொழ என இருக்கும். அதில் எப்படி நிலையாக இருக்கும் ஒரு துளையைப் போடமுடியும்?

மையத்தின் ஈர்ப்பு

வெறும் கற்பனையில் மட்டுமே பூமியைத் துளைத்து அதன் மையப் புள்ளி வழியாக பூமியின் மறுபக்கம் வரும்படி துளை போட முடியும். ஆயினும், ஒரு பேச்சுக்காக அவ்வாறு செய்தால் என்னவாகும் என்பதுதான் கலிலியோ முதலான விஞ்ஞானிகள் தம்மைத் தாமே கேட்டுக்கொண்ட கற்பனைக் கேள்வி.

பூமியின் தரை மீது ஈர்ப்பு விசை நொடிக்கு 9.8 மீட்டர். ஆனால் பூமியின் உள்ளே செல்லச் செல்லத் தலைக்கு மேலே ஓரளவு பூமியும் காலுக்குக் கீழே ஓரளவு பூமியும் இருக்கும் அல்லவா? தலைக்கு மேலே உள்ள உள்ள பூமி நம்மைப் பூமியின் மையத்துக்கு எதிர்த்திசையில் நமது தலையை இழுக்கும். காலுக்குக் கீழ் உள்ள பூமி, மையம் நோக்கி நமது கால்களை இழுக்கும்.

துளையின் உள்ளே இருக்கும் போது ஏற்படும் ஈர்ப்பு விசை நொடிக்கு 9.8 மீட்டர் என்று இருக்காது. உள்ளே செல்லச் செல்லக் காலுக்கு அடியில் உள்ள பூமிப்பகுதி குறைந்து போவதால் ஈர்ப்பு விசையும் குறைந்து போகும். சரியாக பூமியின் மையத்தில் ஈர்ப்பு விசை இருக்கவே இருக்காது.

சடன் பிரேக்

பூமியின் துளை வழியே கல்லை போட்டால் அது உள்ளே விழ, விழ ஈர்ப்பு விசை குறைந்து குறைந்து போனாலும், அதுவரை பெற்ற முடுக்கு வேகம் (acceleration) காரணமாக பூமியின் நடுப்புள்ளியை அடையும் தறுவாயில் அதன் வேகம் நொடிக்கு 8 கி.மீ. என தலைதெறிக்கும் வேகத்தில் செல்லும் எனவும் கலிலியோ கணிதம் செய்தார். இந்த வேகத்தில் சென்றால் சென்னையிலிருந்து திருச்சி செல்ல வெறும் ஒரு நிமிடம்தான் ஆகும்.

பூமியின் நடுப்புள்ளியை அடைந்த கல் என்னவாகும்? கல்லை இழுக்கும் இரண்டு எதிரும் புதிருமான விசைகள் ஒன்றை ஒன்று அழிக்கும். இறுதியில் எந்த ஈர்ப்பு விசையும் இருக்காது. அதனால், பூமியின் மையத்தை அடைந்த கல் அங்கேயே இருந்து விடுமா? இல்லை என்றார் கலிலியோ. சடார் என்று பஸ்ஸில் பிரேக் போட்டால் நாம் முன்னே சாய்ந்து விழுவது போல, தலைதெறிக்கும் வேகத்தில் பூமியின் மையத்தை அடையும் கல் அதன் திணிவு வேகம் தரும் (momentum) உந்துதல் காரணமாகத் தொடர்ந்து பாயும்.

42 நிமிடங்கள்தான்

காற்றின் உராய்வு இல்லை எனக் கொண்டால், பெற்ற உந்துதல் காரணமாக அந்தக் கல் பூமியின் மறுமுனையில் வெளியேறும். ஆனால், வெளியேறிய கல், ‘மேலே எறிந்த கல், அதிகப் பட்ச உயரம் சென்று ஒரு கணம் நின்று கீழே விழுவது போல’ மறுபடி அதே துளையில் விழும். மறுபடி பூமியின் ஈர்ப்பு விசையால் மையம் நோக்கிக் கவரப்படும். முதலில் ஏற்பட்டது போல முடுக்கு வேகம் பெறும். புறப்பட்ட இடம் அடையும். இவ்வாறு மாறி மாறி இருமுனைக்கும் சென்று ஊஞ்சல் போல ஊசல் செய்யும் என்றார் 1632- ல் கலிலியோ.

ஒரு முனையிலிருந்து கல் மறு முனைக்கு 42 நிமிடங்களில் சென்று விடும் என்றார்கள் விஞ்ஞானிகள். சிறிய கல்லும், பெரிய கல்லும் ஒரே வேகத்தில் தான் செல்லும். எனவே, பூமியின் துளைக்குள் விழும் எல்லாம் 42 நிமிடம் 12 நொடியில் மறுமுனையை அடைந்து விடும்.

கற்பிதங்கள்

இந்தக் கணிதத்தில் மூன்று கற்பிதங்களைச் செய்துள்ளோம். ஒன்று பூமியின் துளைக்குள் காற்று உராய்வு இருக்காது என்பது. பூமியின் சுழற்சியால் ஏற்படும் விளைவுகளைக் கணக்கில் கொள்ளாதது இரண்டாவது. பூமியில் உள்ள திணிவு எல்லாப் பகுதி யிலும் சரிசமமாக இறைந்து கிடக்கிறது என்பது மூன்றாவது கற்பிதம்.

காற்று உராய்வைக் கணக்கில் கொண்டால் என்ன ஆகும்? அப்போதும் கல்லுக்கு பூமியின் மையத்தைக் கடந்து செல்லப் போதிய திணிவுவேகம் இருக்கும். ஆனால் முழுமையாகப் பூமியின் மறுபுறத்தைக் கல் எட்டாது. சற்றே நடுவழியில் மீண்டும் பூமியின் மையத்தை நோக்கி விழத் தொடங்கும். இவ்வாறு ஒவ்வோர் ஊசலிலும் பூமியின் மையத்திலிருந்து உயரே செல்லும் தொலைவு படிப்படியாகக் குறைந்து, குறைந்து இறுதியில் பூமியின் மையத்தில் மிதக்கும்.

இரண்டாவது கற்பிதம் குறித்து

1679-ல் நியூட்டன் சிந்தனை செய்தார். வட துருவத்திலிருந்து தென் துருவம்வரை துளை போட்டால் பூமி சுற்றினாலும் சுற்றாவிட்டலும் விளைவு ஒன்றுதான் என்றார். வேறு இடத்தில் துளை செய்து கல்லைப் போட்டால், கல் விழும் நேரத்தில் பூமி சுற்றுவதால் துளையின் சுவற்றில் கீழே விழும் கல் மோதிவிடும் என்றார் .

துளையில் கல் விழும்போது அதன் பாதை பூமியின் பார்வையில் வளையும். எனவே, துளையின் சுவற்றில் மோதும். நிலநடுக்கோட்டின் அருகேதான் பூமி சுற்றுவதால் வளையும் கல்லின் பாதை மிக அதிகமாக இருக்கும் என கணித்தார் அவர். துளையைச் சுமார் 300 கி.மீ. அகலமான சுரங்கம் அளவுக்குப் போட்டால் நிலநடுக்கோட்டின் அருகிலும் சுவற்றில் மோதாமல் கல் விழும் என்றார்.

மூன்றாவது கற்பிதம்

மூன்றாவது கற்பிதம் குறித்து இப்போதுதான் சிந்தனை செய்துள்ளனர். பூமியில் திணிவு எல்லா இடங்களிலும் சரிசமமாக கன மீட்டருக்கு 5500 கிலோகிராம் எனக் கொண்டால் மட்டுமே மேலே கூறிய கணக்கு சரி வரும். பூமியின் தரைப்பரப்புக்கு அருகில் கன மீட்டருக்கு 1000கிலோகிராம் என்று உள்ள திணிவு, பூமியின் மையத்தின் அருகே சுமார் 13,000 கிலோகிராம் என சில மடங்குகள் அதிகமாக உள்ளது என நிலநடுக்கத்தின்போது எடுத்த ஆய்வுகள் தெரிவிக்கின்றன.

38 நிமிடம்தான்

இதைக் கணக்கில் கொண்டு கணித்தால் என்ன என்று யோசித்தார் கனடா மே கில் பல்கலைக்கழக ஆய்வு மாணவர் அலெக்சாண்டர் க்ளோத்ஸ் (Alexander Klotz). அவர் 42 நிமிடம் 12 நொடி என்பதற்குப் பதிலாக, 38 நிமிடம் 11 நொடிதான் தேவை எனக் கண்டுபிடித்தார்.

இதில்தான் வியப்பு. பூமியில் பகிர்ந்துகிடக்கிற அதன் உண்மையான திணிவைக் கணக்கில் கொண்டு செய்தால் வரும் விடையும், பூமி முழுவதும் சரிசமமாகத் திணிவு பரவிக்கிடக்கிறது என்று போலியாகக் கற்பிதம் செய்தால் வரும் கணிதமும் சற்றேறக்குறைய ஒரே அளவுதான். இதுதான் க்ளோத்ஸ் உட்படப் பல விஞ்ஞானிகளை வியக்கச் செய்துள்ளது.

இது எப்படி? பூமியில் உள்ள திணிவு பகிர்வின் காரணமாகப் பூமியின் உள்ளே செல்லச் செல்ல ஈர்ப்பு விசை சற்றேறக்குறைய சரிசமமாகத்தான் இருக்கிறது. பூமியின் மையக்கரு பகுதியில் ஈர்ப்பு புலம் அங்கு உள்ள மிகு திணிவு காரணமாக அதிகரிக்கிறது. ஆனால் மையம் நோக்கிச் செல்லும் நமது கல் வெகு வேகமாகச் செல்வதால் பூமியின் மையத்தில் குறைவான நேரமே பயணிக்கும். எனவே கல்லின் இயக்கத்தில் பெரிய பாதிப்பு இல்லை, எனவே பெரிய அளவு மாறுபாடு இல்லை என்கிறார் க்ளோத்ஸ். ஆக, பூமியில் துளையும் போட்டு கல்லையும் போட்டுப் பார்த்தாகிவிட்டது.

தொடர்புக்கு: tvv123@gmail.com